最近は「グラフ」、ようはネットワークのことですが、
の話題をいろいろな所で目にします。
何か数理科学的な問題を考える上で、
その表現の幅が豊かであるためでしょうか。
しかし一方で、
それぞれのグラフがどんなグラフなのか、
その「性質」をヒトコトで言うのはなかなか
難しいようです。
そんな中、ある本を読んでいて、
グラフでもやはり「行列式」が
一定の意味のある働きをしているようで、
これにそこはかとない快さを感じました。
この理解を改めて整理したく、
要点を簡潔にまとめてみたいと思います。
結論を先取りすると、
グラフについてある表現をしたとき、
グローバルな性質の1つである行列式が、
結局、木の数になるということ。
この木の数というのが、
電気回路などで重要視される、
(あるいは自分だったら因果とかでも
気にする因子ですが、)
ある種の閉路の数にも一致するというのです。
その読んでいたのは
『線形代数とネットワーク』という本で、
改めて線形代数の価値を感じることになり、
なかなかの良さがあります。
さてこれらを理解するうえで、
見る勉を行うだけだけだとやっぱり記号の意味を
つどつど忘れてしまって面倒です。
さりとてノートに記載していても
少し時間が経つと、どっかいってしまう・・・。
このため、せっかくなので、
記事にまとめて残してみようと思います。
記号を整理する
記号の意味
まずは などの記号の意味を列挙します。
自分で理解しやすい表現にするため、
定義を厳密に記載しているものではありません。
は接続行列。
全ての頂点と枝の組み合わせです。
(隣接行列は頂点と頂点の組み合わせなので、
そこが違いますね。)
頂点 から 枝
が出ていっている場合、
は 1 になります。
入ってきている場合は -1 になります。
『線形代数とネットワーク』38P にある
下図グラフの例を、以下で示します。
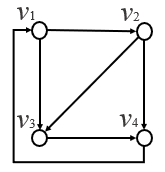
接続行列は、
と表されます。
→行→ が 1つの頂点に相当します。
ここでは丁度4行ありますね。
↓
列
↓
が1つの枝に相当します。
どの列も流出元 1、流入先 -1 が1つずつありますね。
被約接続行列 というものもあります。
から適当な一行を削除します。
ここでは4行目を削除します。
は名前はついていませんが、
頂点の数 に対し
の枝を選ぶ、
部分グラフになります。
というのが既に木の片鱗を見せていますね。
ここで から下図の黒い線だけ選び、
部分グラフ を作ると、
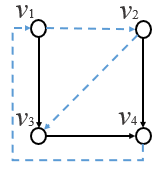
は
となります。
元の のうち、
1 から数えて 3, 4, 5 番目の枝を取っています。
は、
の中の特別な場合で、
「全域木」に相当する場合です。
全域木とは何かというと、うまく
「全ての頂点を含む木」を取り出した
部分グラフですね。
連結なグラフであれば必然的に、
上手に枝を刈っていけば、
かならずすべての頂点を結ぶ木が得られる、
という寸法ですね。
グラフの中に全域木という大きな木が
必然的に含まれているわけです。
なお は補木と呼ばれる、
の全ての枝の集合を表します。
全域木 に補木
の枝
を1つだけつけたときに
現れる単純閉路を と書きます。
少し寄り道になりますが、
以下のタイセット、カットセットというのも
のちに繋がってきます。
の集合を基本タイセットと言います。
対し、 の集合は、
基本カットセットと呼ばれます。
全域木 から枝
だけを除くと、
木は2つの木に分裂していしまいます。
これらの2つの木の頂点の集合を、それぞれ
と書きましょう。
このとき、 を結ぶ完全二部グラフを作ると
(ただし全て から
への向き)、
これがカットセット になります。
基本タイセットを行列表示したのが で、
何番目の閉路が(行)、何番目の枝を(列)
どっち向きに使うか、という行列です。
対して、
基本カットセットを行列表示したのが です。
何番目の二部グラフが(行)、何番目の枝を(列)
どっち向きに使うか、という行列です。
他の頻出記号には があります。
これは とも書け、
グラフラプラシアンのようです。
は長方形の行列ですが、
転置して自分と書けることで相殺し、
少し疎に広く広がっていたのが
キュッと縮まるイメージですね。
同書には無向の例しかなかったのですが、
上図の有向な の例で
を求めると、
・・・何のことはない、
無向のときと同じものですね。
すなわちラプラシアンの -1 倍というわけです。
記号の直感的理解
ここまでで、以下の記号を書いてきました。
少し自分なりに意味を考えてみたいと思います。
まず は、最初だけ戸惑いますが、
文字通り頂点から枝への流出ですね。
隣接行列のあいだに枝が割って入っている、
そういう印象を受けます。
については実用的な要請から
少し振り返ってみます。
は
の行列で、
→1行→が1つの頂点、
↓1列↓が1つの枝になっています。
行なので頂点のほうがちょっと多いですね。
そこで被約にして頂点を1個外してしまえば、
この は
の正方行列です。
全域木 の場合は、(特に根を外す慣例のようですが、)
残された頂点と枝とで1対1対応を作れます。
この対応順で の並びを構成してやれば、
対角成分は皆 になります。
全体のなかで
になる要素の数が
より少ないことを合わせると、
行列式が となることが分かりますね。
すべては木だった
さて、閉路を含むような任意のグラフを考えるさいも、
その中に隠れている木(の数)こそが
グローバルな特徴量の1つである行列式と
なんと一致するのだと、
この本を読んでいて分かってきました。
木が世界を規定するという
北欧神話的なロマンを感じます。
ともあれ、明確に定量化できる量である
行列式が、このような定性的な意味を持つのは、
ひとまずは頼もしさを感じるところです。
ちょっと導き方を確認したうえで、
その上で少し触れたタイセット等とも
関係性をさらってみましょう。
ラプラシアンから1行目と1列目を削った
行
列の
は、
を使って
=
と書けます。
さてこのとき、 はどうでしょうか。
一般に、こういう という
「長方形の行列同士の積」の行列式を考えるとき、
コーシー - ビネの公式が役立つそうです。
本だけだとちょっと読み取れなかったですが、
Wikipedia 情報に頼るとするならば、
専用の項目があって結構詳しく書いてあります。
つまり、 個のうち大小関係を入れ替えない
個を選んで正方形を作ろうというわけですね。
いわゆる 通りを考えるということでしょうか。
確かに、余因子展開を思い出してみれば
確かにそうなるという気がします。
個の取り合わせを
とするなら、
という具合です。
これを の場合で書くと、
となります。
木でないものも含む 全体というのが丁度、
個の取り合わせ全体になっているためですね。
すると、 が閉路を含んでいるときは 0 になるので、
結局 は可能な全域木の数
の数に一致してしまうのですね。
嬉しいことに、というかなんと不思議なことに、
この の行列式及び木の数というのは、
とも
とも
一致してしまうというのです。
さいごに
さて、ここまで、
グラフが行列式といった線形代数的な道具で
それなりにうまく特徴づけられるということを
『線形代数とネットワーク』を通じて
見てきました。
さらに同書では、これらの性質を使って、
閉路を1周したとき電圧の和がゼロになることや、
回路方程式の性質までを
みごとに書き下しています。
が、この記事の目的は、
あくまで特徴量の意味を読み解くことであり、
またあまりに本の詳細を書いてしまうのは
マナー違反でもあるでしょうから、
少なくとも前半部分については、
ここまでにしたいと思います。
私のこの興奮を共有したい意味でも、
是非『線形代数とネットワーク』を
おススメしたいです!
さて、グラフの特徴ということで、
その片鱗の一部を掴めたようには思います。
しかしグラフの特徴というのは
さらに色々な方法による広がりがあり、
ありていにいえば、
まだその隆盛は始まったばかりともいえるでしょう。
例えば機械学習なんかではもちらん、
グラフを取り扱いを容易にするという方法論自体が
1つの大きなテーマというわけです。
これからの動向も楽しみですね。
それではここまで、
ありがとうございました。
またネットワーク上のどこかで、
お会いしましょう。
参考文献
ogyahogya.hatenablog.com
※ 最終アクセス:2019/08/06

- 作者: ??金久
- 出版社/メーカー: 日本評論社
- 発売日: 2017/03/08
- メディア: 単行本
- この商品を含むブログを見る

- 作者: 山室静
- 出版社/メーカー: 社会思想社
- 発売日: 1962/07
- メディア: 文庫
- 購入: 2人 クリック: 5回
- この商品を含むブログ (10件) を見る
ja.wikipedia.org
※ 最終アクセス:2019/08/06
mathtrain.jp
※ 最終アクセス:2019/08/06